Основные определения статики

Статика

Статика — раздел механики, изучающий условия равновесия тел под действием приложенных сил. В статике рассматриваются системы, которые находятся в состоянии покоя или движутся равномерно и прямолинейно.

Основная задача статики: определение условий, при которых тело остается в равновесии под действием системы сил.

Виды равновесия

Устойчивое равновесие

После выведения тела из равновесия равнодействующая сила стремится вернуть его в исходное положение.

Пример: Шар в углублении, маятник в положении покоя.

Неустойчивое равновесие

После выведения тела из равновесия равнодействующая сила продолжает удалять его от положения равновесия.

Пример: Шар на выпуклой поверхности, карандаш, стоящий на острие.

Безразличное равновесие

Перемещение тела не изменяет условий равновесия, тело остается в равновесии при любом положении.

Пример: Шар на горизонтальной плоскости, колесо на оси.

Линия действия силы

Линия действия силы — прямая, проходящая через точку приложения силы вдоль её вектора. Это важное понятие в статике, так как оно позволяет применять принцип переноса силы вдоль линии её действия.

Принцип переноса силы

Точку приложения силы можно переносить вдоль линии её действия без изменения механического состояния тела. Равновесие при этом не нарушается.

Важно: Этот принцип справедлив только для абсолютно твёрдых тел и не применим к деформируемым телам.

Условия равновесия

Первое условие равновесия

Векторная сумма всех сил, действующих на тело, равна нулю:

\sum \vec{F} = 0

Это условие обеспечивает отсутствие поступательного движения.

Второе условие равновесия

Алгебраическая сумма моментов всех сил относительно любой оси равна нулю:

\sum M = 0

Это условие обеспечивает отсутствие вращательного движения.

Примечание: Для равновесия тела должны выполняться оба условия одновременно.

Практическое применение

В архитектуре и строительстве

Расчет устойчивости зданий и сооружений
Проектирование мостов и кранов
Определение центра тяжести конструкций
Анализ распределения нагрузок

В технике и механике

Конструирование машин и механизмов
Расчет опор и подвесных систем
Анализ устойчивости транспортных средств
Проектирование стационарных установок

Визуальное сравнение устойчивого, неустойчивого и безразличного равновесия на примере шара на различных поверхностях — Рис.1. Виды равновесия: устойчивое, неустойчивое и безразличное

Графическое представление линии действия силы и принципа переноса точки приложения силы вдоль этой линии — Рис.2. Линия действия силы и принцип переноса

Момент силы. Условия равновесия

Момент силы

Момент силы — физическая величина, характеризующая вращательное действие силы на тело. Он определяет способность силы вызывать вращение тела вокруг оси или точки.

M = F \cdot d

Момент силы [Н·м]

Сила [Н]

Плечо силы [м]

Плечо силы

Плечо силы — кратчайшее расстояние от оси вращения до линии действия силы. Чтобы найти плечо силы:

Выбрать ось вращения
Провести прямую вдоль направления силы
Опустить перпендикуляр от оси вращения к проведённой прямой

Правило знаков: Момент считают положительным, если сила стремится поворачивать тело против часовой стрелки, и отрицательным, если по часовой стрелке.

Векторное представление момента силы

Момент силы — векторная величина. В трёхмерном пространстве момент силы определяется как векторное произведение:

\vec{M} = \vec{r} \times \vec{F}

Момент силы [Н·м]

Радиус-вектор [м]

Сила [Н]

Правило правой руки: Если представить, что мы взяли тело в правую руку и пытаемся его повернуть в направлении, куда указывают четыре пальца (силы, пытающиеся повернуть тело направлены по направлению этих пальцев), то оттопыренный большой палец покажет в ту сторону, куда направлен вращающий момент (момент этих сил).

Условия равновесия

1. Для материальной точки

Если тело движется только поступательно или может быть представлено как материальная точка, то для равновесия достаточно равенства нулю суммы всех действующих сил:

\sum \vec{F} = \vec{F_1} + \vec{F_2} + \dots + \vec{F_n} = \vec{0}

2. Для тела с неподвижной осью вращения

Если тело может только вращаться вокруг неподвижной оси, то оно будет находиться в равновесии, когда сумма моментов сил относительно этой оси равна нулю:

\sum M = M_1 + M_2 + \dots + M_n = 0

3. Для твёрдого тела общего случая

Для твёрдого тела, способного и к поступательному, и к вращательному движению, равновесие достигается при одновременном выполнении двух условий:

\begin{cases} \sum \vec{F} = \vec{0} \\ \sum \vec{M} = \vec{0} \end{cases}

Важно: Для полного равновесия твёрдого тела должны выполняться оба условия одновременно — равенство нулю суммы всех сил и равенство нулю суммы всех моментов сил.

Практическое применение

Простые механизмы

Рычаги и балансиры
Блоки и полиспасты
Ворота и лебёдки
Гаечные ключи и инструменты

Инженерия и строительство

Расчёт балок и опор
Проектирование кранов и подъёмников
Анализ устойчивости конструкций
Расчёт фундаментов и опорных узлов

Примеры расчета

Рычаг первого рода

Ось вращения расположена между точками приложения сил. Условие равновесия:

F_1 \cdot d_1 = F_2 \cdot d_2

Рычаг второго рода

Ось вращения расположена с одного конца, силы приложены по одну сторону от оси. Условие равновесия:

F_1 \cdot d_1 = F_2 \cdot d_2

Визуальное сравнение рычагов первого, второго и третьего рода — Рис.3. Типы рычагов: первого, второго и третьего рода

Демонстрация условий равновесия для рычага: изменение моментов сил при перемещении грузов — Рис.4. Условия равновесия для рычага

Визуализация распределения моментов сил в балке с различными опорами и нагрузками — Рис.5. Условия равновесия для балки

Центр масс и центр тяжести

Центр масс и центр тяжести — важные понятия в механике, которые помогают описывать движение тел и их равновесие. Хотя эти понятия тесно связаны, они имеют различные физические интерпретации.

Центр масс

Центр масс — точка, которая характеризует распределение массы в теле. Она движется так, как если бы вся масса тела была сосредоточена в этой точке, и все внешние силы были приложены к ней.

Определение: Геометрическая точка, положение которой зависит только от распределения масс в теле.

Центр тяжести

Центр тяжести — точка приложения равнодействующей силы тяжести, действующей на тело. В этой точке можно считать сосредоточенной всю силу тяжести тела.

Определение: Точка приложения равнодействующей сил тяжести, действующих на все части тела.

Формулы для расчета центра масс

В векторной форме

\vec{r}_c = \frac{\sum m_i\vec{r}_i}{\sum m_i}

Координата X

x_c = \frac{\sum m_ix_i}{\sum m_i}

Координата Y

y_c = \frac{\sum m_iy_i}{\sum m_i}

Координата Z

z_c = \frac{\sum m_iz_i}{\sum m_i}

r_c

Радиус-вектор центра масс

m_i

Масса i-й точки

r_i

Радиус-вектор i-й точки

x_i, y_i, z_i

Координаты i-й точки

Особенности и свойства

Однородное поле тяжести

В однородном поле силы тяжести центр масс совпадает с центром тяжести. Это справедливо для тел, размеры которых малы по сравнению с размерами Земли.

Симметричные тела

Для симметричных тел центр масс (центр тяжести) расположен в геометрическом центре тела, на оси симметрии или в плоскости симметрии.

Составные тела

Для системы тел центр масс рассчитывается как среднее взвешенное положений центров масс отдельных тел, где весами являются их массы.

Движение центра масс

Центр масс системы движется как материальная точка с массой, равной сумме масс всех тел системы, под действием всех внешних сил.

Практическое применение

В технике

Расчет устойчивости транспортных средств
Проектирование летательных аппаратов
Балансировка вращающихся деталей
Проектирование спортивного инвентаря

В архитектуре

Расчет устойчивости зданий и сооружений
Проектирование подвесных конструкций
Анализ распределения нагрузок
Проектирование мостов и кранов

Методы определения центра тяжести

Аналитический метод

Использование формул для расчета координат центра масс на основе известного распределения масс.

Экспериментальный метод

Подвешивание тела в разных точках и определение пересечения вертикальных линий.

Метод симметрии

Использование свойств симметрии тела для определения положения центра тяжести.

Центр масс гири: демонстрация положения центра масс относительно геометрического центра тела — Рис.6. Центр масс гири

Статика жидкостей и газов

Статика жидкостей и газов (гидростатика и аэростатика) — раздел механики, изучающий равновесие жидкостей и газов и действие неподвижных жидкостей и газов на погруженные в них тела.

Особенность: Жидкости и газы передают давление во всех направлениях, что отличает их от твердых тел и приводит к особым закономерностям.

Закон Паскаля

Основной закон гидростатики, открытый Блезом Паскалем в 1653 году:

Давление, производимое на жидкость или газ, передается без изменения в каждую точку жидкости или газа

Следствие: Жидкости и газы передают оказываемое на них давление по всем направлениям одинаково во все точки жидкости или газа.

Практическое применение

Гидравлические прессы и домкраты
Тормозные системы автомобилей
Пневматические системы
Водопроводные системы

Формула гидравлического пресса

\frac{F_1}{S_1} = \frac{F_2}{S_2}

где F₁, F₂ — силы, S₁, S₂ — площади поршней

Давление и сила давления

Давление

Скалярная физическая величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности.

P = \frac{F}{S}

Давление [Па]

Сила [Н]

Площадь [м²]

Сила давления

Сила, с которой жидкость или газ действует на поверхность тела.

F = P \cdot S

Важно: Сила давления всегда направлена перпендикулярно поверхности и равномерно распределена по ней.

Гидростатическое давление

Давление в жидкости, обусловленное её весом. Зависит только от плотности жидкости и высоты столба жидкости над рассматриваемой точкой.

P = \rho g h

Давление [Па]

Плотность [кг/м³]

Ускорение свободного падения [м/с²]

Высота столба [м]

Особенность: Гидростатическое давление не зависит от формы сосуда, а только от плотности жидкости и высоты её столба.

Полное давление в жидкости

Полное давление в жидкости складывается из внешнего давления (обычно атмосферного) и гидростатического давления.

P = P_0 + \rho g h

Полное давление [Па]

P₀

Атмосферное давление [Па]

ρgh

Гидростатическое давление [Па]

Нормальное атмосферное давление: 101325 Па ≈ 10⁵ Па = 100 кПа = 760 мм рт. ст.

Закон Архимеда

На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу вытесненной жидкости или газа.

F_A = \rho g V

F_A

Сила Архимеда [Н]

Плотность жидкости [кг/м³]

Ускорение свободного падения [м/с²]

Объем вытесненной жидкости [м³]

Условия плавания тел

F_A > mg — тело всплывает
F_A = mg — тело плавает внутри жидкости или на поверхности
F_A < mg — тело тонет

Применение

Судостроение и проектирование плавательных средств
Аэронавтика и воздухоплавание
Гидрометрия и измерение плотности веществ
Подводные аппараты и оборудование

Распределение давления в жидкости: зависимость давления от глубины и иллюстрация закона Паскаля — Рис.7. Давление в жидкости

Действие выталкивающей силы Архимеда на тело, погруженное в жидкость: направление и величина силы — Рис.8. Выталкивающая сила (сила Архимеда)

Сообщающиеся сосуды и гидравлический пресс

Сообщающиеся сосуды и гидравлический пресс — важные применения законов гидростатики, демонстрирующие передачу давления в жидкостях и позволяющие усиливать приложенные силы.

Основной принцип: Оба устройства основаны на законе Паскаля, согласно которому давление, производимое на жидкость, передается без изменения во все точки жидкости.

Сообщающиеся сосуды

Сообщающиеся сосуды — система соединенных между собой сосудов, в которых жидкость может свободно перетекать из одного сосуда в другой. Это свойство широко используется в технике и быту.

Условие равновесия

P_0 + \rho_1 g h_1 = P_0 + \rho_2 g h_2

P₀

Атмосферное давление [Па]

ρ₁, ρ₂

Плотности жидкостей [кг/м³]

Ускорение свободного падения [м/с²]

h₁, h₂

Высоты столбов жидкостей [м]

Однородная жидкость

Уровень поверхности однородной жидкости в сообщающихся сосудах устанавливается на одинаковой высоте, независимо от формы и сечения сосудов.

Разные жидкости

При использовании разных жидкостей высота столба каждой жидкости обратно пропорциональна её плотности:

\frac{h_1}{h_2} = \frac{\rho_2}{\rho_1}

Применение: Водопроводные системы, водяные уровни, чайники, кофейники, шлюзы, гидравлические системы.

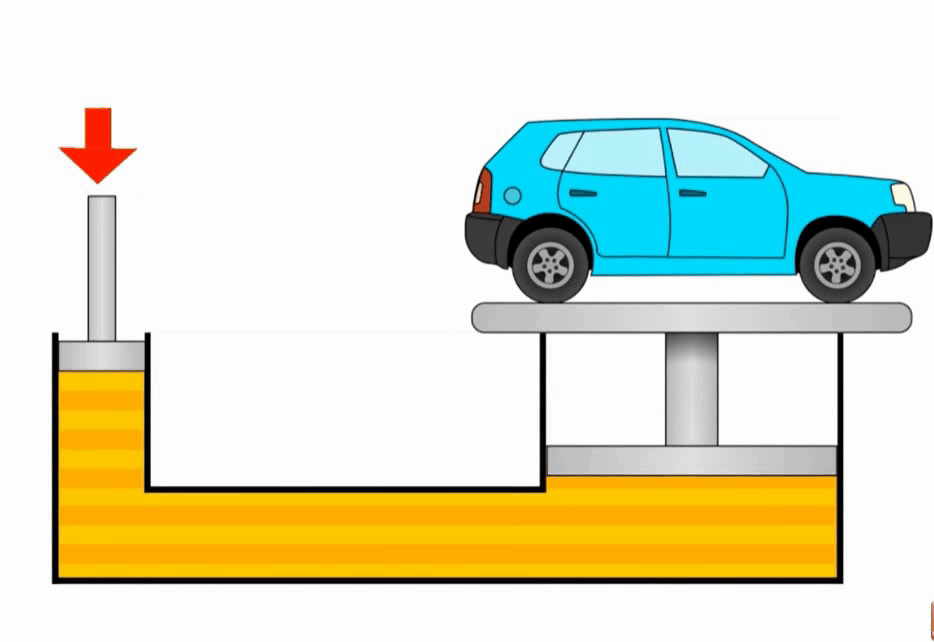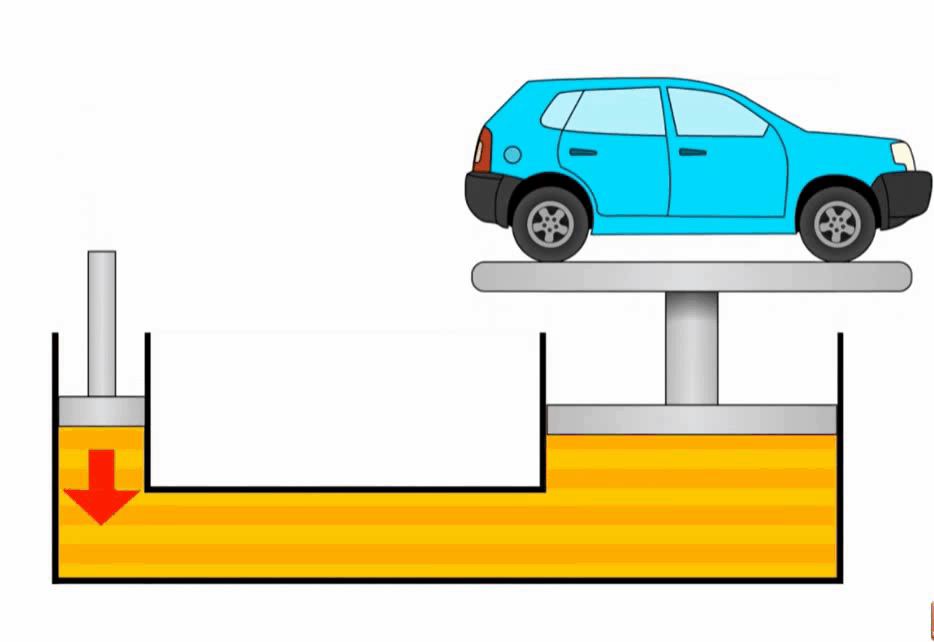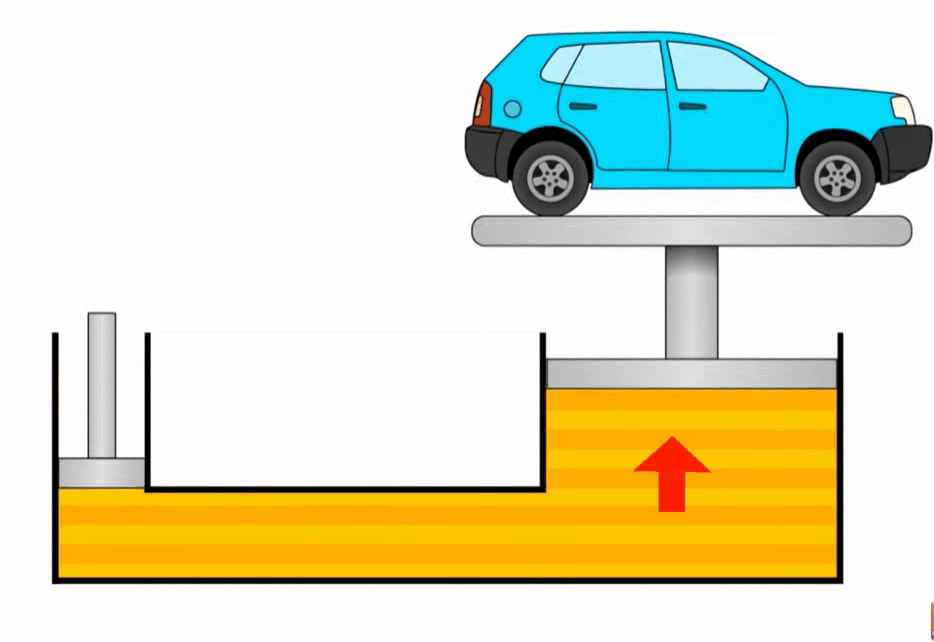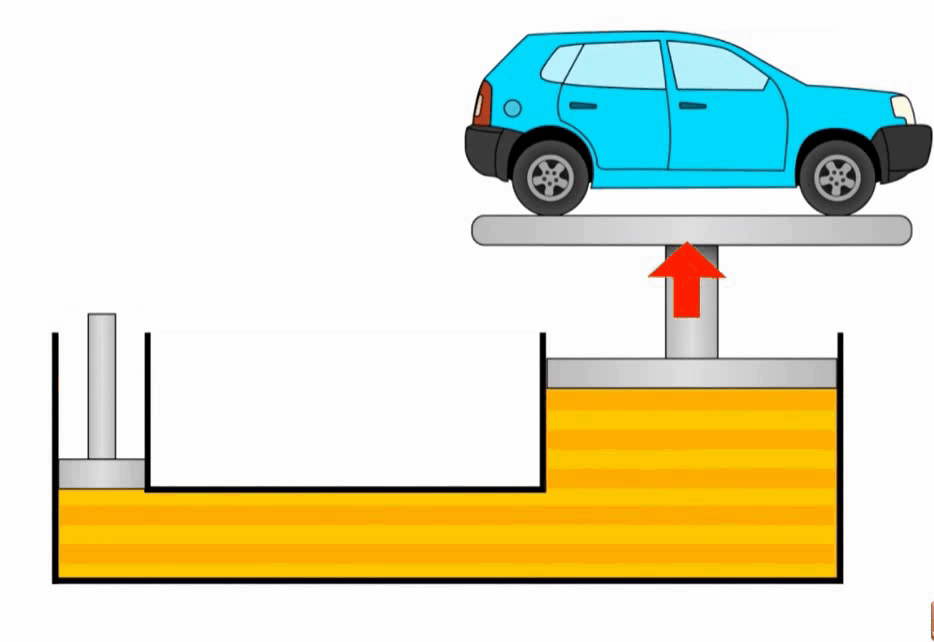
Гидравлический пресс

Гидравлический пресс — устройство, основанное на законе Паскаля, позволяющее получать выигрыш в силе за счет разницы площадей поршней. Он состоит из двух цилиндрических сообщающихся сосудов, заполненных жидкостью и закрытых поршнями разной площади.

Основной принцип

\frac{F_1}{S_1} = \frac{F_2}{S_2}

F₁

Сила на малом поршне [Н]

S₁

Площадь малого поршня [м²]

F₂

Сила на большом поршне [Н]

S₂

Площадь большого поршня [м²]

Выигрыш в силе

F_2 = F_1 \cdot \frac{S_2}{S_1}

Во сколько раз площадь большого поршня больше площади малого, во столько раз сила на большом поршне больше силы на малом.

Проигрыш в расстоянии

h_1 \cdot S_1 = h_2 \cdot S_2

Перемещение поршней обратно пропорционально их площадям. Гидравлический пресс не дает выигрыша в работе.

С учетом КПД

В реальных условиях необходимо учитывать потери энергии на трение и другие факторы:

F_2 = \eta \cdot F_1 \cdot \frac{S_2}{S_1}

КПД системы

F₁

Сила на малом поршне [Н]

S₂/S₁

Отношение площадей

F₂

Сила на большом поршне [Н]

Золотое правило механики: Гидравлический пресс не дает выигрыша в работе. Во сколько раз выигрываем в силе, во столько раз проигрываем в расстоянии.

Практическое применение

Сообщающиеся сосуды

Водопроводные и отопительные системы
Гидравлические системы автомобилей (тормоза, сцепление)
Водяные уровни в строительстве
Чайники, кофейники, лейки
Шлюзы и судоходные каналы
Сифоны и гидрозатворы

Гидравлический пресс

Прессы для обработки металлов (штамповка, ковка)
Прессы для производства изделий из пластмасс
Гидравлические домкраты и подъемники
Тормозные системы тяжелой техники
Прессы для брикетирования отходов
Медицинское оборудование (зубоврачебные кресла)

Историческая справка

Сообщающиеся сосуды

Принцип сообщающихся сосудов был известен еще в древности. Римские акведуки, построенные в III веке до н.э., использовали этот принцип для подачи воды в города.

Гидравлический пресс

Гидравлический пресс был изобретен английским механиком Джозефом Брама в 1795 году. Его изобретение стало возможным благодаря открытию закона Паскаля в 1653 году.

Интересные факты

Рекорды мощности

Современные гидравлические прессы могут развивать усилие до 80 000 тонн, что используется для штамповки крупных деталей авиационной и космической техники.

В природе

Принцип сообщающихся сосудов наблюдается в кровеносной системе человека и животных, где давление крови выравнивается по всем сосудам.

Сообщающиеся сосуды с однородной и разнородной жидкостью: принцип установления уровней жидкости — Рис.8. Сообщающиеся сосуды

Схема гидравлического пресса: принцип работы, соотношение сил и перемещений поршней — Рис.9. Гидравлический пресс