Основные определения динамики

Введение в динамику

Динамика — раздел механики, изучающий причины движения тел и взаимодействие между ними. В отличие от кинематики, которая описывает движение, динамика объясняет, почему тела движутся именно так.

Основные понятия

Свободное тело

Тело, на которое не действуют другие тела или их воздействия скомпенсированы. Свободное тело сохраняет состояние покоя или равномерного прямолинейного движения.

Инертность

Свойство тел сохранять состояние покоя или равномерного прямолинейного движения. Мера инертности тела — его масса.

Масса (m)

Количественная мера инерционных и гравитационных свойств тела.

m = \rho V

где ρ — плотность тела [кг/м³], V — объём тела [м³]

Свойства массы: аддитивна, инвариантна (не зависит от скорости), сохраняется в замкнутых системах.

Механические системы и силы

Типы систем

Механическая система

Совокупность тел, взаимодействующих между собой посредством сил.

Замкнутая система

Система, на которую не действуют внешние силы или их действие скомпенсировано.

Изолированная система

Система, не взаимодействующая с другими системами.

Типы сил

Внутренние силы

Силы взаимодействия между телами механической системы.

Внешние силы

Силы, действующие на систему со стороны тел, не входящих в неё.

Консервативные силы

Силы, работа которых не зависит от формы траектории.

Сила и её представление

Сила как вектор

Сила — векторная величина, характеризующая взаимодействие тел. Измеряется в ньютонах [Н].

\vec{F} = F_x\vec{i} + F_y\vec{j} + F_z\vec{k}

Разложение силы на проекции по координатным осям.

Модуль и направление

|\vec{F}| = \sqrt{F_x^2 + F_y^2 + F_z^2}

\cos\alpha = \frac{F_x}{|\vec{F}|}

\cos\beta = \frac{F_y}{|\vec{F}|}

\cos\gamma = \frac{F_z}{|\vec{F}|}

Равнодействующая сила и принцип суперпозиции

\vec{F}_{\text{р}} = \sum_{i=1}^n \vec{F}_i = \vec{F}_1 + \vec{F}_2 + \dots + \vec{F}_n

Равнодействующая сила — векторная сумма всех сил, действующих на тело.

Принцип суперпозиции сил

Действующие на тело силы можно заменить их векторной суммой без изменения результата воздействия.

Системы отсчета

Инерциальная система отсчета

Система, в которой свободное тело сохраняет состояние покоя или равномерного прямолинейного движения.

Пример: неподвижный вагон метро, лаборатория на поверхности Земли (приближенно).

Неинерциальная система отсчета

Система, движущаяся с ускорением относительно инерциальной. В такой системе свободное тело движется с ускорением.

Пример: вагон метро, набирающий скорость, вращающаяся карусель.

Принцип относительности Галилея

Все механические явления протекают одинаково во всех инерциальных системах отсчета при одинаковых начальных условиях.

Следствие: Законы механики инвариантны относительно преобразований Галилея. Нельзя определить, находится ли инерциальная система в покое или движется равномерно и прямолинейно, с помощью механических экспериментов.

Практическое значение

В физике

Основы для формулировки законов Ньютона, понимания инерции, разработки классической механики.

В технике

Расчет движения транспортных средств, проектирование механизмов, анализ устойчивости конструкций.

В астрономии

Описание движения небесных тел, расчет орбит, понимание гравитационных взаимодействий.

В повседневной жизни

Объяснение явлений инерции, понимание принципов безопасности при движении, проектирование спортивного инвентаря.

Инерциальная система отсчёта: примеры систем, где свободное тело сохраняет состояние покоя или равномерного движения — Рис. 1. Инерциальная система отсчёта

Неинерциальная система отсчёта: примеры систем, движущихся с ускорением — Рис. 2. Неинерциальная система отсчёта

Законы Ньютона

Первый закон Ньютона (Закон инерции)

Существуют системы отсчёта, называемые инерциальными, в которых тело сохраняет состояние покоя или равномерного прямолинейного движения, пока внешние силы не заставят его изменить это состояние.

Ключевой принцип: Если равнодействующая всех сил равна нулю, ускорение тела также равно нулю.

Второй закон Ньютона (Основной закон динамики)

В инерциальных системах отсчёта ускорение тела (a) прямо пропорционально равнодействующей всех приложенных к нему сил (F) и обратно пропорционально его массе (m).

\vec{F} = m\vec{a}

где F — равнодействующая сила [Н], m — масса тела [кг], a — ускорение [м/с²]

Следствия

Направление ускорения совпадает с направлением равнодействующей силы
При нулевой равнодействующей тело сохраняет состояние покоя или равномерного движения
Закон выполняется только в инерциальных системах отсчёта

Особенности

Для протяжённых тел уравнение записывается для центра масс
В неинерциальных системах необходимо учитывать силы инерции
Сила является причиной, ускорение — следствием

Алгоритм решения задач

Выбрать инерциальную систему отсчёта
Определить все силы, действующие на тело
Выбрать удобные координатные оси
Разложить силы на составляющие по осям
Записать уравнения движения для каждой оси
Решить полученную систему уравнений

Третий закон Ньютона (Закон действия и противодействия)

Силы взаимодействия двух тел равны по модулю, противоположны по направлению и приложены к разным телам.

\vec{F}_{1 \to 2} = -\vec{F}_{2 \to 1}

где F_1→2 — сила, с которой первое тело действует на второе,
F_2→1 — сила, с которой второе тело действует на первое

Особенности

Силы возникают парами при взаимодействии
Силы приложены к разным телам
Силы одной природы
Силы не компенсируют друг друга

Примеры

Сила реакции опоры
Сила гравитационного притяжения
Сила упругости пружины
Сила трения между поверхностями

Важно: Силы действия и противодействия никогда не компенсируют друг друга, так как приложены к разным телам.

Практическое применение законов Ньютона

В технике

Расчет прочности конструкций
Проектирование транспортных средств
Создание систем стабилизации
Разработка робототехники

В повседневной жизни

Объяснение явления инерции
Понимание принципов безопасности
Проектирование спортивного инвентаря
Анализ дорожно-транспортных происшествий

Историческая справка

Законы Ньютона были сформулированы английским ученым Исааком Ньютоном и опубликованы в его фундаментальном труде "Математические начала натуральной философии" в 1687 году.

Интересный факт: Первый закон Ньютона является развитием идей Галилея о инерции, которые тот сформулировал на 50 лет раньше.

Визуализация Второго закона Ньютона: зависимость ускорения от силы и массы — Рис. 3. Второй закон Ньютона: F = ma

Иллюстрация Третьего закона Ньютона: взаимодействие двух тел с силами равной величины и противоположного направления — Рис. 4. Третий закон Ньютона: действие равно противодействию

Сила упругости

Деформация и её виды

Упругая деформация

Деформация, которая полностью исчезает после прекращения действия внешних сил. Тело возвращается к первоначальным размерам и форме.

Пластическая деформация

Деформация, которая сохраняется после прекращения действия внешних сил. Тело не возвращается к первоначальным размерам и форме.

Сила упругости

Сила, возникающая при упругой деформации тела и направленная в сторону, противоположную смещению частиц.

Особенности

Действует между слоями деформированного тела
Приложена к каждому слою деформированного тела
В точке контакта тел направлена перпендикулярно их поверхностям
Для пружин, нитей, тросов и стержней направлена вдоль их осей

Закон Гука

Модуль силы упругости прямо пропорционален величине деформации.

F = k |\Delta x|

Сила упругости [Н]

Коэффициент жёсткости [Н/м]

Δx

Изменение длины [м]

Примечание: Знак минус в формуле $F = -k \Delta x$ указывает на противоположное направление силы упругости относительно деформации.

Коэффициент жёсткости

k = \frac{E S}{L_0}

Жёсткость [Н/м]

Модуль Юнга [Па]

Площадь сечения [м²]

L₀

Длина [м]

Важно: При разрезании пружины пополам жёсткость каждой части увеличивается вдвое, так как длина уменьшается вдвое.

Соединения пружин

Последовательное соединение

\frac{1}{k_{\text{общ}}} = \frac{1}{k_1} + \frac{1}{k_2}

k_{\text{общ}} = \frac{k_1 k_2}{k_1 + k_2}

Общая жёсткость уменьшается. Деформация распределяется между пружинами.

Параллельное соединение

k_{\text{общ}} = k_1 + k_2

Общая жёсткость увеличивается. Деформация пружин одинакова.

Потенциальная энергия упругой деформации

При сжатии или растяжении пружина приобретает потенциальную энергию, которая может быть преобразована в кинетическую энергию.

W = \frac{k (\Delta x)^2}{2}

Потенциальная энергия [Дж]

Коэффициент жёсткости [Н/м]

Δx

Деформация [м]

Применение: Эта формула используется при расчёте энергии в механических системах, пружинных маятниках и различных механизмах.

Практическое применение

В технике

Амортизаторы транспортных средств
Пружинные механизмы часов
Бамперы и буферы
Подвесные системы

В быту

Матрасы с пружинами
Канцелярские зажимы
Спортивный инвентарь
Игрушки и механизмы

Графическое представление деформации пружины под действием силы — Рис.5. Деформация пружины и сила упругости

Схема последовательного и параллельного соединения пружин с обозначением сил и деформаций — Рис.6. Последовательное и параллельное соединение пружин

Силы тяготения, тяжести, реакции опоры и вес тела

Сила гравитационного притяжения (тяготения)

Фундаментальная сила природы, с которой притягиваются любые два тела, обладающие массой. Эта сила определяет движение планет, звезд и галактик во Вселенной.

F = G \frac{m_1 m_2}{r^2}

Сила притяжения [Н]

6.674·10^-11 Н·м²/кг²

m₁, m₂

Массы тел [кг]

Расстояние между центрами [м]

Примечание: Формула справедлива для однородных шаров или когда одно тело — шар, а второе можно считать материальной точкой.

Сила тяжести

Частный случай силы гравитационного притяжения — сила, с которой планета притягивает к себе тела, находящиеся вблизи ее поверхности.

\vec{F}_\text{т} = m \vec{g}

F_т

Сила тяжести [Н]

Ускорение свободного падения [м/с²]

На Земле: g ≈ 9.8 м/с², но может незначительно изменяться в зависимости от географической широты и высоты над уровнем моря.

Ускорение свободного падения

Ускорение, которое приобретает тело под действием только силы тяжести. Зависит от массы и радиуса планеты.

У поверхности планеты:

g = G \frac{M}{R^2}

Масса планеты [кг]

Радиус планеты [м]

Гравитационная постоянная

На высоте h от поверхности:

g = G \frac{M}{(R+h)^2}

Высота над поверхностью [м]

Вес тела и сила реакции опоры

Вес тела — сила, с которой тело действует на опору или подвес вследствие гравитационного притяжения. Всегда приложен к опоре, а не к телу!

Вес тела

По третьему закону Ньютона:

\vec{P} = -\vec{N}

где N — сила реакции опоры

Особенности веса

Измеряется в Ньютонах [Н]
Зависит от ускорения опоры
Может быть больше или меньше силы тяжести
Может быть равен нулю (невесомость)

Важно: Не путайте массу (постоянная величина, измеряется в кг) и вес (сила, зависящая от условий, измеряется в Н).

Невесомость и условие отрыва

Невесомость

Состояние, когда сила реакции опоры равна нулю:

N = 0

Тело не давит на опору, исчезает ощущение веса. Возникает при свободном падении, на орбите, в самолете, летящем по параболической траектории.

Условие отрыва тела от поверхности

Тело отрывается от поверхности, когда:

N \leq 0

Это происходит, когда ускорение движения вверх превышает ускорение свободного падения, либо когда тело достигает первой космической скорости.

Практическое применение

В астрономии и космонавтике

Расчет орбит спутников и планет
Определение масс небесных тел
Космические полеты и невесомость
Гравитационные маневры

В повседневной жизни

Взвешивание тел (весы измеряют вес, а не массу)
Проектирование строительных конструкций
Геодезия и гравиметрическая разведка
Спорт (прыжки, бег, гимнастика)

Гравитационная сила притяжения между двумя телами — Рис.7. Гравитационная сила притяжения

Сила реакции опоры и вес тела — Рис.8. Сила реакции опоры и вес

Сила трения

Трение и его виды

При перемещении одного тела относительно другого возникает явление трения — сила сопротивления относительному движению, возникающая на границе соприкосновения тел.

Внешнее (сухое) трение

Возникает при взаимодействии соприкасающихся твёрдых тел без смазки. Подразделяется на трение покоя, скольжения и качения.

Внутреннее (вязкое) трение

Возникает при движении тел в жидкостях и газах. Зависит от скорости движения и свойств среды.

Сила трения покоя

Возникает, когда к телу прикладывают силу, но оно остаётся неподвижным. Её величина равна модулю приложенной силы и направлена противоположно возможному движению.

F_{\text{тр.пок}} \leq \mu_{\text{пок}} \cdot N

F_тр.пок

Сила трения покоя [Н]

μ_пок

Коэффициент трения покоя

Сила реакции опоры [Н]

Особенности: В школьных задачах максимальное значение силы трения покоя обычно принимают равным силе трения скольжения, хотя в действительности оно несколько больше.

Сила трения скольжения

Возникает при движении тела относительно поверхности под действием внешних сил. Всегда направлена противоположно направлению движения.

F_{\text{тр.ск}} = \mu_{\text{ск}} \cdot N

F_тр.ск

Сила трения скольжения [Н]

μ_ск

Коэффициент трения скольжения

Сила реакции опоры [Н]

Свойства трения скольжения:

Не зависит от площади контакта (для большинства материалов)
Не зависит от скорости (при малых скоростях)
Зависит от материалов и состояния поверхностей
Коэффициент трения скольжения обычно меньше коэффициента трения покоя

Сила трения качения

Возникает при качении тел без проскальзывания. Обычно значительно меньше силы трения скольжения.

F_{\text{тр.кач}} = \mu_{\text{кач}} \cdot \frac{|\vec{N}|}{R}

F_тр.кач

Сила трения качения [Н]

μ_кач

Коэффициент трения качения [м]

Радиус катящегося тела [м]

Применение: Благодаря малой силе трения качения оно широко используется в технике (колеса, подшипники, ролики).

Сила вязкого трения

Возникает при движении тел в жидкостях и газах. Зависит от скорости движения, формы тела и свойств среды (вязкости, плотности).

При малых скоростях

F_{\text{тр.вязк}} = \beta v

Сила пропорциональна скорости (формула Стокса). Характерно для медленного движения небольших тел в вязких жидкостях.

При больших скоростях

F_{\text{тр.вязк}} = \xi v^2

Сила пропорциональна квадрату скорости. Характерно для быстрого движения тел в жидкостях и газах (автомобили, самолеты, падающие тела).

Коэффициент линейного сопротивления [Н·с/м]

Коэффициент квадратичного сопротивления [Н·с²/м²]

Практическое применение

Полезное трение

Ходьба и бег (трение между подошвой и поверхностью)
Тормозные системы транспортных средств
Зажимные механизмы и инструменты
Письмо ручкой на бумаге

Борьба с трением

Смазочные материалы в механизмах
Подшипники (замена трения скольжения на трение качения)
Обтекаемые формы для уменьшения сопротивления воздуха
Полировка поверхностей

Типичные коэффициенты трения

Материалы	Трение покоя (μ_пок)	Трение скольжения (μ_ск)
Дерево по дереву	0.25-0.5	0.2-0.4
Металл по металлу	0.15-0.2	0.1-0.15
Резина по асфальту (сухое)	0.9-1.1	0.7-0.9
Лёд по льду	0.05-0.1	0.03-0.05

Рис.10. Сила трения качения и вязкое трение

Закон Архимеда и давление

Закон Архимеда

На погруженное в жидкость (или газ) тело действует выталкивающая сила, равная весу жидкости (или газа), вытесненной этим телом. Открыт древнегреческим учёным Архимедом в III веке до н.э.

F_A = \rho g V

F_A

Сила Архимеда [Н]

Плотность жидкости/газа [кг/м³]

Объём вытесненной жидкости [м³]

Условия плавания тел

ρ_тела > ρ_{жидкости}

Тело тонет

F_A < F_тяж

ρ_тела = ρ_{жидкости}

Тело плавает внутри жидкости

F_A = F_тяж

ρ_тела < ρ_{жидкости}

Тело всплывает

F_A > F_тяж

Важно: В невесомости сила Архимеда равна нулю, так как отсутствует вес жидкости!

Гидростатическое давление

Давление, создаваемое весом столба жидкости. Распределяется одинаково во всех направлениях (закон Паскаля) и увеличивается с глубиной.

P = \rho g h

Гидростатическое давление [Па]

Плотность жидкости [кг/м³]

Высота столба жидкости [м]

Закон Паскаля: Давление, производимое на жидкость или газ, передается в любую точку без изменения во всех направлениях.

Давление в жидкости

Полное давление в жидкости складывается из атмосферного давления и гидростатического давления.

P_{\text{полн}} = P_{\text{атм}} + \rho g h

P_полн

Полное давление [Па]

P_атм

Атмосферное давление [Па]

ρgh

Гидростатическое давление [Па]

Давление и сила давления

Давление

Скалярная физическая величина, показывающая силу, действующую на единицу площади.

P = \frac{F}{S}

Сила, перпендикулярная поверхности [Н]

Площадь поверхности [м²]

Сила давления

Сила, с которой жидкость или газ действует на поверхность.

F = P \cdot S

Для расчета силы давления жидкости на дно или стенки сосуда используйте формулу F = P·S, где P — давление на данной глубине.

Происхождение силы Архимеда

Сила Архимеда возникает из-за разности гидростатических давлений на нижнюю и верхнюю поверхности погруженного тела. Давление на нижнюю поверхность (P_сн) больше, чем на верхнюю (P_св), что создает результирующую выталкивающую силу.

F_A = F_{\text{сн}} - F_{\text{св}} = (P_{\text{сн}} - P_{\text{св}}) \cdot S

F_сн

Сила с которой давит жидкость на тело снизу [Н]

F_св

Сила с которой давит жидкость на тело сверху [Н]

Практическое применение

В технике

Конструирование судов и подводных лодок
Гидравлические прессы и домкраты
Водопроводные системы
Аэродинамика и проектирование летательных аппаратов

В природе и быту

Плавание рыб и морских животных
Воздухоплавание (воздушные шары, дирижабли)
Измерение плотности веществ (ареометры)
Водные виды спорта и отдыха

Единицы измерения давления

Единица	Обозначение	Соотношение
Паскаль	Па (Pa)	1 Па = 1 Н/м²
Миллиметр ртутного столба	мм рт. ст.	1 мм рт. ст. ≈ 133,322 Па
Бар	бар (bar)	1 бар = 10⁵ Па
Атмосфера	атм (atm)	1 атм ≈ 101325 Па

Сила Архимеда, действующая на погруженное тело — Рис.11. Сила Архимеда

Гидростатическое давление в зависимости от глубины — Рис.12. Гидростатическое давление

Импульс. Закон сохранения импульса. Абсолютно упругий и неупругий удар

Импульс тела

Импульс (количество движения) — векторная физическая величина, являющаяся мерой механического движения тела. Чем больше масса и/или скорость движения тела, тем больше его импульс, а значит, тем большее воздействие тело способно оказать на другие тела при взаимодействии с ними.

\vec{p} = m\vec{v}

Импульс тела [кг·м/с]

Масса тела [кг]

Скорость тела [м/с]

Импульс системы и изменение импульса

Импульс системы тел

\vec{p}_{\text{сист}} = \sum_{i=1}^n \vec{p}_i = \sum_{i=1}^n m_i\vec{v}_i

Векторная сумма импульсов всех тел, входящих в систему.

Изменение импульса

\Delta\vec{p} = \vec{F}\Delta t

Произведение силы на время её действия называется импульсом силы [Н·с].

Важно: Если равнодействующая сила равна нулю, то импульс тела не изменяется.

Закон сохранения импульса

Фундаментальный закон природы: при любых взаимодействиях в замкнутой системе тел импульс системы остается постоянным.

\vec{p}_1 + \vec{p}_2 + \cdots + \vec{p}_n = \text{const}

Для системы из двух тел (проекция на ось OX)

m_1 v_{1x} + m_2 v_{2x} = m_1 u_{1x} + m_2 u_{2x}

m₁, m₂

Массы тел [кг]

v₁, v₂

Скорости до удара [м/с]

u₁, u₂

Скорости после удара [м/с]

Проекция на ось OX

Абсолютно упругий удар

Удар, при котором сохраняются и импульс, и кинетическая энергия системы. Тела после соударения движутся отдельно друг от друга.

\begin{cases} m_1\vec{v}_1 + m_2\vec{v}_2 = m_1\vec{u}_1 + m_2\vec{u}_2 \\ \dfrac{m_1 v_1^2}{2} + \dfrac{m_2 v_2^2}{2} = \dfrac{m_1 u_1^2}{2} + \dfrac{m_2 u_2^2}{2} \end{cases}

Примеры

Столкновение бильярдных шаров
Соударение молекул газа
Упругие шары

Особенности

Сохраняется механическая энергия
Тела не деформируются
Отсутствуют потери энергии

Абсолютно неупругий удар

Удар, при котором сохраняется импульс системы, но не сохраняется кинетическая энергия. Тела после соударения движутся как единое целое.

m_1\vec{v}_1 + m_2\vec{v}_2 = (m_1 + m_2)\vec{u}

Потеря энергии

Q = \Delta E_k = E_{k\text{нач}} - E_{k\text{кон}}

Потерянная энергия преобразуется в тепло, работу деформации или другие виды энергии.

Примеры

Столкновение пластилиновых шаров
Пуля, застревающая в мишени
Падение груза на платформу

Особенности

Происходит деформация тел
Часть энергии превращается в тепло
Тела движутся вместе после удара

Сравнение типов ударов

Характеристика	Упругий удар	Неупругий удар
Сохранение импульса	✓ Сохраняется	✓ Сохраняется
Сохранение энергии	✓ Сохраняется	✗ Не сохраняется
Деформация тел	Упругая (исчезает)	Пластическая (сохраняется)
Движение после удара	Тела движутся раздельно	Тела движутся вместе
Коэффициент восстановления	e = 1	e = 0

Практическое применение

В технике

Расчет движения ракет и реактивных снарядов
Проектирование амортизаторов и буферных систем
Кузовной ремонт автомобилей
Спортивное оборудование (мячи, клюшки)

В науке и природе

Изучение столкновений элементарных частиц
Моделирование движения небесных тел
Исследование биомеханики (ходьба, бег, прыжки)
Анализ дорожно-транспортных происшествий

Реактивное движение

Частный случай закона сохранения импульса. Движение тела возникает благодаря отделению от него с некоторой скоростью части его массы.

m\vec{v} = (m - \Delta m)(\vec{v} + \Delta\vec{v}) + \Delta m\vec{u}

где Δm — масса отделившейся части, u — скорость отделившейся части относительно тела.

Абсолютно упругий удар двух шаров с сохранением энергии — Рис.13. Абсолютно упругий удар

Абсолютно неупругий удар двух шаров с потерей энергии — Рис.14. Абсолютно неупругий удар

Энергия. Работа. Закон сохранения энергии

Энергия и её формы

Энергия — фундаментальная физическая величина, характеризующая способность тела или системы совершать работу. Энергия не возникает из ничего и не исчезает бесследно, а лишь преобразуется из одной формы в другую.

Основные формы энергии

Механическая
Тепловая
Электромагнитная
Химическая
Ядерная

Единицы измерения

Джоуль (Дж) — основная единица
Электрон-вольт (эВ) — в атомной физике
Каллория (кал) — в теплотехнике
Киловатт-час (кВт·ч) — в электроэнергетике

Механическая энергия

Механическая энергия — энергия, связанная с движением тел или их положением в поле сил. Она складывается из кинетической и потенциальной энергии.

E = E_k + E_p

Полная механическая энергия [Дж]

E_k

Кинетическая энергия [Дж]

E_p

Потенциальная энергия [Дж]

Кинетическая энергия

Энергия движения тела:

E_k = \frac{mv^2}{2}

Масса [кг]

Скорость [м/с]

Потенциальная энергия

Энергия взаимодействия тел:

E_p = mgh

Масса [кг]

Ускорение свободного падения [м/с²]

Высота [м]

Виды потенциальной энергии

Упругая деформация

E_p = \frac{k (\Delta x)^2}{2}

Жёсткость [Н/м]

Δx

Деформация [м]

Гравитационное взаимодействие

E_p = -G\frac{m_1 m_2}{r}

6.67·10⁻¹¹ Н·м²/кг²

m₁, m₂

Массы [кг]

Расстояние [м]

Примечание: Знак минус означает, что тела притягиваются друг к другу.

Работа силы

A = \vec{F} \cdot \vec{s} = Fs\cos\alpha

Работа [Дж]

Сила [Н]

Перемещение [м]

Угол между F и s

Положительная работа

0° ≤ α < 90°

Сила способствует движению

Нулевая работа

α = 90°

Сила перпендикулярна перемещению

Отрицательная работа

90° < α ≤ 180°

Сила препятствует движению

Свойство: Работа равнодействующей силы равна сумме работ всех приложенных к телу сил.

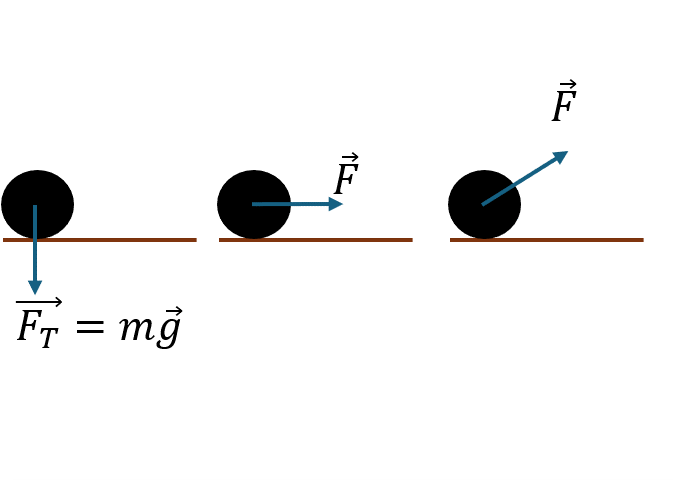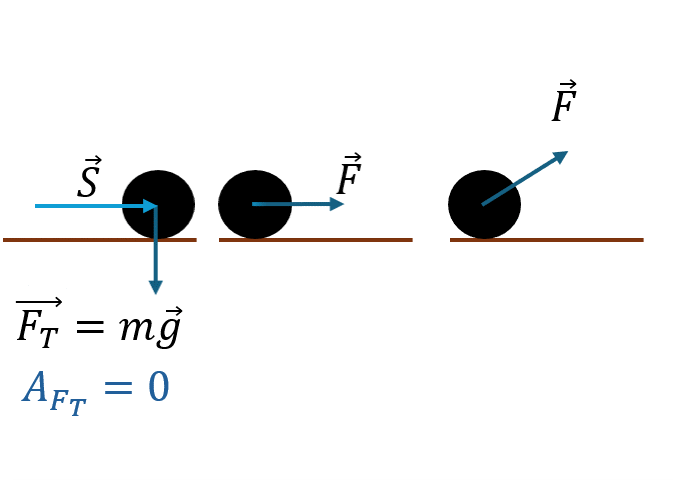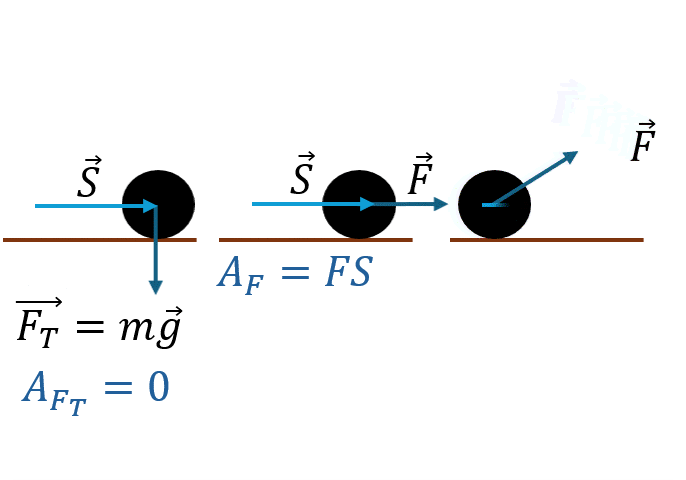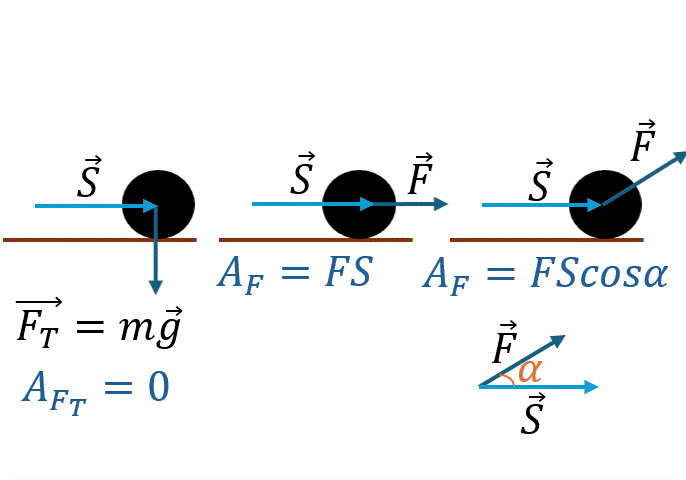
Законы сохранения и изменения энергии

Закон сохранения механической энергии

Если в замкнутой системе действуют только консервативные силы (гравитация, упругость), то полная механическая энергия системы сохраняется.

E_k + E_p = \text{const}

Пример: Движение маятника в вакууме, движение планет.

Закон изменения механической энергии

Если в системе действуют неконсервативные силы (трение, сопротивление), то изменение механической энергии равно работе этих сил.

\Delta E = A_{\text{тр}}

Пример: Торможение автомобиля, затухание колебаний маятника.

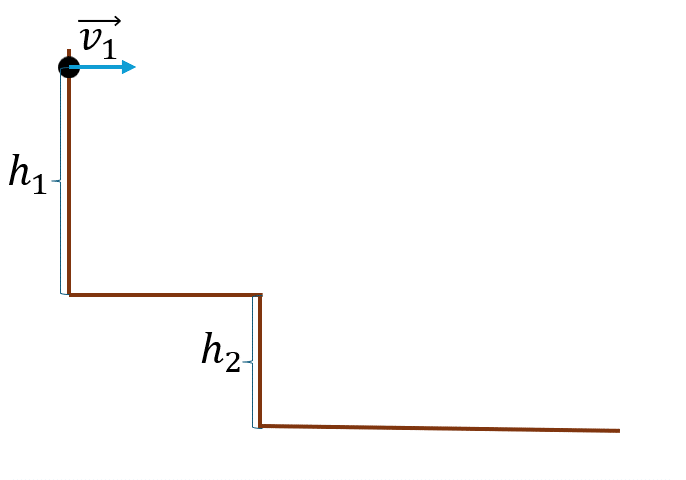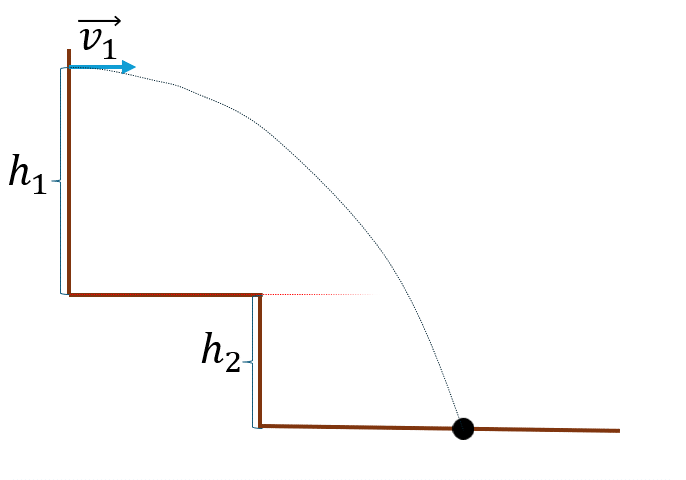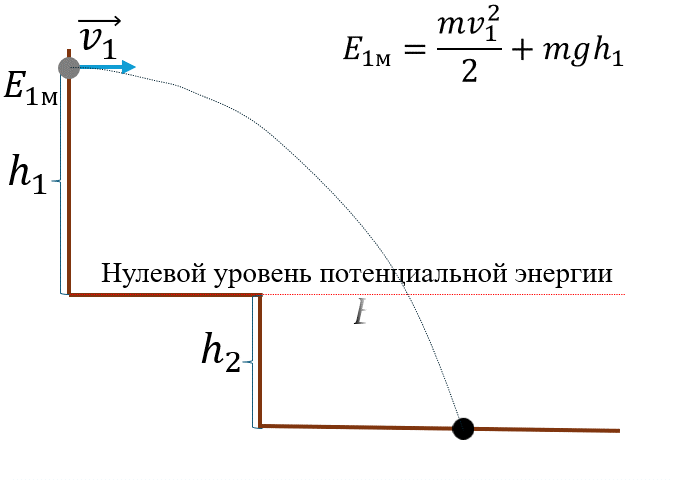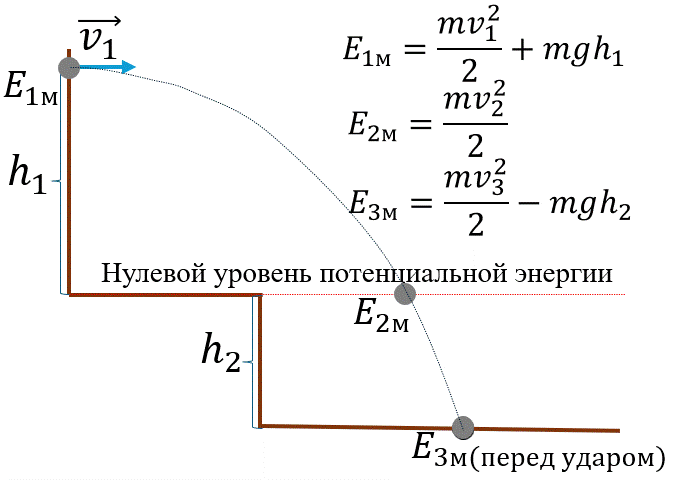
Теорема об изменении кинетической энергии

Изменение кинетической энергии тела равно работе всех сил, приложенных к телу.

\Delta E_k = A_{\text{всех сил}}

Практическое применение

В технике

Расчет КПД механизмов
Проектирование энергоэффективных систем
Создание аккумуляторов энергии
Разработка тормозных систем

В природе

Круговорот воды в природе
Движение небесных тел
Энергетические процессы в живых организмах
Преобразование энергии в экосистемах

Демонстрация работы силы: зависимость работы от угла между силой и перемещением — Рис.15. Работа силы

Преобразование энергии: переход потенциальной энергии в кинетическую и обратно — Рис.16. Преобразование энергии

Мощность. Мгновенная мощность. КПД

Мощность

Мощность — физическая величина, характеризующая скорость выполнения работы или преобразования энергии. Показывает, какая работа совершается за единицу времени или какая энергия передаётся системе за единицу времени.

P = \frac{A}{\Delta t} = \frac{Q}{\Delta t}

Мощность [Вт]

Работа [Дж]

Теплота [Дж]

Δt

Время [с]

Единицы измерения: Ватт (Вт) = Дж/с. В технике часто используют киловатты (1 кВт = 1000 Вт) и лошадиные силы (1 л.с. ≈ 735 Вт).

Мгновенная мощность

Мгновенная мощность — мощность в данный момент времени, определяемая как скалярное произведение вектора силы на вектор мгновенной скорости.

P = \vec{F} \cdot \vec{v} = Fv\cos\alpha

Мощность [Вт]

Сила [Н]

Скорость [м/с]

Угол между F и v

Максимальная мощность

α = 0° (cosα = 1)

Сила и скорость сонаправлены

Нулевая мощность

α = 90° (cosα = 0)

Сила перпендикулярна скорости

Отрицательная мощность

α > 90° (cosα < 0)

Сила препятствует движению

Коэффициент полезного действия (КПД)

КПД — безразмерная величина, характеризующая эффективность системы или устройства в преобразовании энергии. Показывает, какая часть подведённой энергии используется полезно.

\eta = \frac{A_{\text{п}}}{A_{\text{з}}} \times 100\%

КПД [%]

A_п

Полезная работа [Дж]

A_з

Затраченная работа [Дж]

КПД через мощность

\eta = \frac{P_{\text{п}}}{P_{\text{з}}} \times 100\%

P_п

Полезная мощность [Вт]

P_з

Затраченная мощность [Вт]

Причины потерь

Трение в движущихся частях
Сопротивление среды
Нагрев проводников
Рассеивание энергии

Примеры КПД

Лампы накаливания: 5-10%
Двигатель автомобиля: 25-30%
Электродвигатель: 70-95%
Фотоэлементы: 15-25%

Важно: КПД всегда меньше 100% из-за неизбежных потерь энергии на трение, нагрев и другие необратимые процессы.

Практическое применение

В технике

Расчет производительности машин
Проектирование энергоэффективных систем
Выбор двигателей для механизмов
Оценка экономичности транспорта

В быту

Выбор бытовой техники
Расчет потребления электроэнергии
Оценка эффективности отопительных систем
Сравнение экономичности ламп освещения

Связь с другими понятиями

Мощность и работа

A = P \cdot \Delta t

Работа равна произведению мощности на время её совершения

Мощность и энергия

E = P \cdot \Delta t

Энергия равна произведению мощности на время